Hunan Adio Electronic Technology Co., Ltd.

How to understand the capacity aging of capacitors

2020-11-13

The capacity and dielectric loss of a ferroelectric ceramic capacitor tend to decay over time. This phenomenon, known as aging, is reversible and occurs because the ferroelectric crystal structure changes with temperature.

Ferrodielectric with barium titanate (BaTiO₃) as the main component, adding certain oxides to change the crystal habits and symmetry of the material, resulting in ferroelectric domains. Near the Curie point (120 ℃), BaTiO₃The crystal structure changes from tetragonal phase to cubic phase, and spontaneous polarization no longer occurs. When the material is cooled through the Curie point, the crystal structure of the material changes from the cubic phase to the tetragonal phase again, and there is no center of symmetry in the lattice structure. Ti⁴Ions can occupy one of two asymmetric positions, resulting in a permanent electric dipole. These galvanic poles are spontaneously generated and slightly ordered since the influence of adjacent unit cell interactions is sufficient to establish the polarization domains. The parallel poled domains are randomly oriented (in the absence of an applied electric field), providing strain energy to the system. The relaxation of strain energy is the cause of the aging of the material's dielectric constant, which has the following time relationship:

　　K = K₀-m log t

Here.

K = dielectric constant at any time t

K₀= time t₀(_t0

m = decay rate

The above formula is a logarithmic relationship. If the data is processed using a semi-logarithmic graph, the result will approximate a straight line, as shown in the following figure. The percentage of K (or capacitance) change in every ten times can be calculated and used as an indicator to measure the quality of porcelain.

The factors that are related to the microstructure and thus influence the polarization (material purity, grain size, sintering, grain boundaries, porosity, internal stress) also determine the degree of freedom of domain wall movement and reorientation.

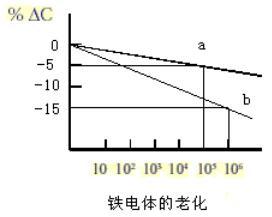
Example (a) Aging rate = -5% / 5 ten times = 1.0/ten times (hours)

Example (B) Aging rate = -15% / 6 times = 2.5/10 times (hours)

It can be seen that the rate of material aging is closely related to the material composition and process, and is also very sensitive to the factors that affect the dielectric constant of the material.

For ferroelectrics, such as X7R, the time loss of capacity is inevitable, although it can be recovered by heating the medium above the Curie point to change the crystal structure of the material back to the "normal" cubic state. But once cooled down, the crystal structure of the material changes to the tetragonal phase again, spontaneous polarization reappears, and the resulting new polarization domains allow the aging process to start again.

Aging phenomena are not observed in paraelectrons, such as COG, since there is no mechanism of spontaneous polarization. The aging rate is affected by the "voltage state" of the capacitor. The device exhibits capacity loss in a high temperature (below the Curie temperature) DC bias load test, but the aging rate is very low. It is theorized that the voltage loading at high temperature promotes the relaxation of the polarization domains. Of course, if the actual temperature exceeds the Curie point, the voltage effect disappears.

Capacitor manufacturers often compensate for the capacity loss of the ferroelectric by adjusting the limit value of the measurement, so that the component will not exceed the tolerance range due to aging after long-term use. For example, for a dielectric material with an aging rate of 1.5% /ten times, the measurement standard needs to be increased to 3%, I .e., two ten times. Components that pass the 100-hour test after being exposed to the Curie temperature point for a long time can still ensure that they will not exceed the tolerance range after another two ten-times, or 10000 hours.